„Low Volatility“ – Outperformance durch niedrigeres Risiko?
Rund um die Theorie der Effizienten Märkte gibt es diverse (sogenannte) Anomalien, die immer wieder diese Theorie selbst in Frage stellen. Momentum ist sicher eine der härtesten, allerdings gibt es kurz nach der Ausrufung dieser Theorie (1970) einen weiteren Faktor, der so gar nicht in das Bild der klassischen Finanzmathematik passt: Der „Low Volatility“ - Faktor.
Im Zusammenhang mit dem „Capital Asset Pricing Model“, welches postuliert, dass höheres Risiko höhere Renditen impliziert, hat sich die Frage ergeben, ob dies wirklich so ist. Jener Fischer Black, der ein Jahr später das sogenannte Black-Scholes Optionspreismodell veröffentlicht, hat hierzu die Antwort mit Scholes und Jensen schon 1972 gegeben („The Capital Asset Pricing Model: Some Empirical Findings“). Ausgehend von Arbeiten aus 1970 (Autoren Friend und Blume) wird festgehalten, dass systematisches Investieren in Aktien mit niedriger Schwankung („Low Volatility“) ausgerechnet (risikoadjustierte) Überrenditen im Vergleich zum Markt erlaubt. Man könnte sagen, dass dies eine Anomalie ist, man könnte sagen, dass Schwankung kein gutes Maß für Risiko ist, man könnte sich fragen, ob nicht indirekte Risiken, die nicht sichtbar sind, vorhanden sind. Man könnte sich allerdings auch fragen, ob nicht Trends wirken und Momentum und Low Volatility vielleicht dieselbe Ursache haben.
„Low Volatility“ und Trends – eine Frage der Skala
Hinsichtlich Momentum hatten wir uns über ein Verfahren der künstlichen Intelligenz gefragt, gibt es Wavelet-Skalen (aus unserem Trendmodell), die diesen Faktor Momentum gut beschreiben? Die gibt es und analog hierzu fragen wir uns, gibt es das bei „Low Volatility“? Wir betrachten nachfolgend eine „Low Volatility“-Strategie, die auf Basis der letzten drei Jahre jeder Aktie die Schwankung in ihrer Rendite zuweist. Das Universum wird dann monatlich „gerankt“ und diejenigen Aktien (zehn Prozent des Marktes), die die geringste Schwankug aufweisen, werden in das Portfolio aufgenommen. Gleichzeitig fragen wir uns anhand des Trendmodells, in welchem wir den zuletzt sichtbaren Trend einer Aktie zu einer gegebenen Wavelet-Skala betrachten, finden wir eine Wavelet-Skala, die anhand des Modells diesen klassischen „Low Volatility“-Faktor gut beschreibt?
 Abbildung 1: In diesem Experiment wird der „Low Volatility“-Faktor (zehn Prozent der am schwächsten schwankenden Aktien gemessen aus der Drei-Jahres-Kurshistorie und mit einem monatlichem Rebalancing) aus einem Universum von 1.100 Aktien repliziert. Hierzu werden über das Trendmodell systematisch monatlich Trends ausgewertet und zehn Prozent der Aktien mit der geringsten Volatilität auf dem zuletzt sichtbaren Trend in das Ziel-Portfolio übernommen. Über ein Verfahren aus der Künstlichen Intelligenz wird die Trendskala so bestimmt, dass die Renditen des klassischen „Low Volatility“-Faktors durch das Trendmodell mit höchster Güte (R2-Wert von 0,98) statistisch hoch-signifikant erklärt werden können.
Abbildung 1: In diesem Experiment wird der „Low Volatility“-Faktor (zehn Prozent der am schwächsten schwankenden Aktien gemessen aus der Drei-Jahres-Kurshistorie und mit einem monatlichem Rebalancing) aus einem Universum von 1.100 Aktien repliziert. Hierzu werden über das Trendmodell systematisch monatlich Trends ausgewertet und zehn Prozent der Aktien mit der geringsten Volatilität auf dem zuletzt sichtbaren Trend in das Ziel-Portfolio übernommen. Über ein Verfahren aus der Künstlichen Intelligenz wird die Trendskala so bestimmt, dass die Renditen des klassischen „Low Volatility“-Faktors durch das Trendmodell mit höchster Güte (R2-Wert von 0,98) statistisch hoch-signifikant erklärt werden können.
Analog zu Momentum finden wir also in diesem Fall eine Skala in unserem Trendmodell, das dieses Phänomen „Low Volatility“ gut beschreibt.
„Low Volatility“ ein Maß für Stabilität von Trends?
Aber wieso schlagen schwach schwankende Aktien den Markt? Wer diese Frage beantworten möchte, sollte sich die Marktcharakteristik ansehen. In den nachfolgenden Abbildungen messen wir den Markt (also alle Aktien des Marktes) aus. Je Aktie und pro vorgegebener Wavelet-Skala messen wir Trends und messen in diesen Trends bestimmte Charakteristiken (wie Länge, Steigung oder Schwankung). Wir bilden über alle Aktien den Mittelwert und wiederholen diesen Prozess für alle Trendzerlegungs-Skalen (Wavelet-Skala):
 Abbildung 2: In diesem Experiment berechnen wir für alle Aktien des Universums die individuellen Trends pro vorgegebener Skala. Für eine einzelne Skala berechnen wir alle Trends aller Aktien und messen die Länge in Börsentagen. Wir unterschieden hier Auf- und Abwärtstrends und berechnen den Mittelwert über alle Aktien des Universums. Diesen Vorgang wiederholen wir für unterschiedliche Granularitäten (Auflösungen bzw. Wavelet-Skalen) und tragen dies von links nach rechts auf. Es wird ersichtlich, dass sich Auf- und Abwärtstrends stark hinsichtlich der Länge in Börsentagen unterscheiden.
Abbildung 2: In diesem Experiment berechnen wir für alle Aktien des Universums die individuellen Trends pro vorgegebener Skala. Für eine einzelne Skala berechnen wir alle Trends aller Aktien und messen die Länge in Börsentagen. Wir unterschieden hier Auf- und Abwärtstrends und berechnen den Mittelwert über alle Aktien des Universums. Diesen Vorgang wiederholen wir für unterschiedliche Granularitäten (Auflösungen bzw. Wavelet-Skalen) und tragen dies von links nach rechts auf. Es wird ersichtlich, dass sich Auf- und Abwärtstrends stark hinsichtlich der Länge in Börsentagen unterscheiden.
Wie man in der Abbildung oben schnell erfasst, Auf- und Abwärtstrends sind drastisch unterschiedlich: Während Aufwärtstrends langsame Bewegungen sind, sind Abwärtstrends kürzere Bewegungen. Aber nicht nur das:
 Abbildung 3: Analog zu Abbildung 2 führen wir dasselbe Experiment wie oben aus, nur, dass wir diesmal die Steigung der Trends (Trenddrift) auswerten. Auch hier gilt: Auf- und Abwärtstrends sind strukturell unterschiedlich.
Abbildung 3: Analog zu Abbildung 2 führen wir dasselbe Experiment wie oben aus, nur, dass wir diesmal die Steigung der Trends (Trenddrift) auswerten. Auch hier gilt: Auf- und Abwärtstrends sind strukturell unterschiedlich.
Wer die Steigungen betrachtet, stellt schnell fest (siehe oben), dass Aufwärtstrends nicht nur längere, sondern auch langsamere Bewegungen (hinsichtlich der Rendite) sind (im Vergleich zu Abwärtstrends, die kürzer und auch schneller sind).
 Abbildung 4: Analog zu Abbildung 2 und 3 führen wir dasselbe Experiment wie oben aus, nur, dass wir diesmal die Schwankung der Trends (Trend Volatilität) auswerten. Auch hier gilt: Auf- und Abwärtstrends sind strukturell unterschiedlich.
Abbildung 4: Analog zu Abbildung 2 und 3 führen wir dasselbe Experiment wie oben aus, nur, dass wir diesmal die Schwankung der Trends (Trend Volatilität) auswerten. Auch hier gilt: Auf- und Abwärtstrends sind strukturell unterschiedlich.
Wer jetzt noch einen Schritt weitergeht und die Schwankung in den letzten Trends betrachtet, der stellt fest, dass Aufwärtstrends auch noch die ruhigeren Bewegungen – im Vergleich zu Abwärtstrends – sind.
„Low Volatility“ – ein indirektes Maß
Ist also „Low Volatility“ ein indirektes Maß? Die Antwort geben wir durch die nächste Grafik.
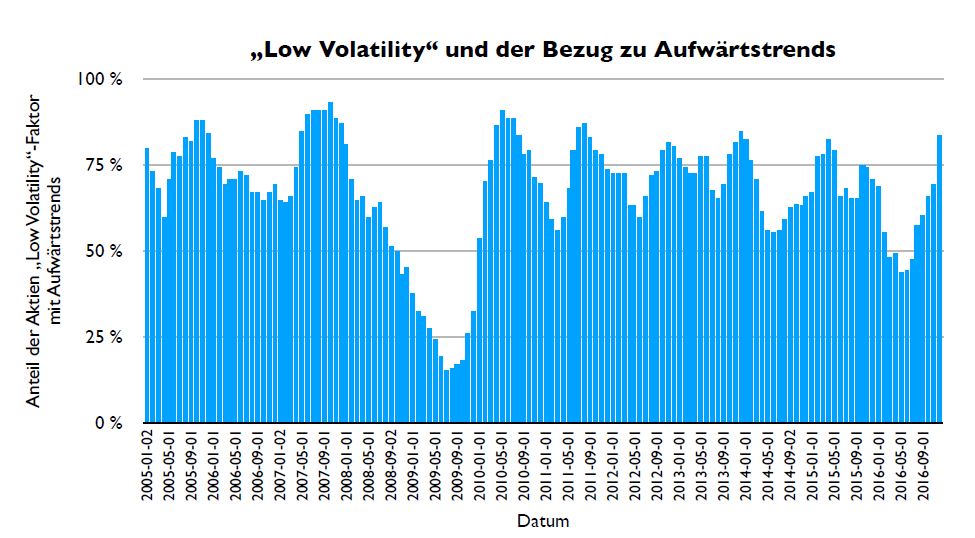 Abbildung 5: Wir replizieren den „Low Volatility“-Faktor und berechnen pro Tag, wie viele Aktien Aufwärtstrends in diesem Faktor-Portfolio aufweisen.
Abbildung 5: Wir replizieren den „Low Volatility“-Faktor und berechnen pro Tag, wie viele Aktien Aufwärtstrends in diesem Faktor-Portfolio aufweisen.
Hier betrachten wir den „Low Volatility“-Faktor durch die Trendbrille (Replikation durch Trendmodell) und fragen uns, wie viele der Aktien eigentlich Aufwärtstrends aufweisen. Wie sich schnell erschließt, sind dies fast durchgängig mehr als 50 Prozent der Aktien. Kurz gesagt, da Aufwärtstrends und Abwärtstrends sehr unterschiedliche Charakteristiken haben, selektiert „Low Volatility“ indirekt Aktien (statistisch und im Mittel) mit stabilen, längeren und langsam ansteigenden Aufwärtstrends. „Outperformance“ wundert daher aus Trendsicht überhaupt nicht nicht. Schon hier kann man von Überlagerungsprozessen am Aktienmarkt sprechen – eine Vermutung, die Benoît Mandelbrot gegen Ende seiner Karriere geäußert hat. In diesem Kontext muss man sich eine vielleicht letzte Frage stellen: Können wir eventuell „Value“-Ansätze analog auffassen? Die Antwort mag überraschen oder auch nicht. Aber davon später mehr…
Lesen Sie hier die vorhergehenden Teile der Serie:
Momentum – ein fundamentaler Faktor
Trends und asymptotisch Effiziente Märkte
So funktionieren die Finanzmärkte
Effiziente Märkte und die Klassik
Sind Märkte wirklich effizient?
Fraktale Märkte: Wie berechnet man einen Trend?
;) Foto: © / funtap / 123RF
Foto: © / funtap / 123RF





